一、单摆

1．定义：如图所示，在细线的一端拴一个小球，另一端固定在悬点上，如果线的伸长和质量都不计，球的直径比摆线短得多，这样的装置叫做单摆。

2．视为简谐运动的条件：①摆角小于5°；②摆线质量远小于小球质量，而可以忽略；③小球半径远小于摆长，摆球可以看成质点。

 

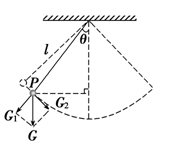
3．回复力：小球所受重力沿圆弧切线方向的分力，即：F=G₂=Gsinθ

在摆角θ很小时，sinθ 近似等于OP弧长比上摆长l ，而OP弧长近似等于x ，得到 F=G₂=Gsinθ=xmg/l，x为摆开的位移，l为摆线长，F 的方向与位移x的方向相反。

4．周期公式：

5．单摆的等时性：单摆的振动周期取决于摆长l和重力加速度g，与振幅和振子（小球）质量都没有关系。

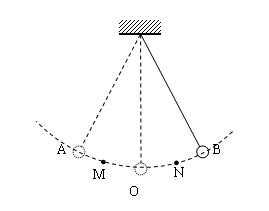
6．对摆长的理解：是指悬点到小球重心的长度，也就是摆线长l’，加上小球的半径r，即l=l’+r。