匀速圆周运动
圆周运动是一种最常见的曲线运动。例如电动机转子、车轮、皮带轮等都作圆周运动。

线速度
做圆周运动的物体单位时间内通过的弧长,表达为v=Δs/Δt,单位m/s。
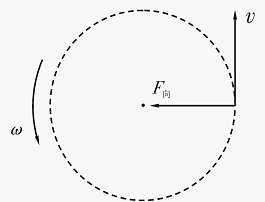
线速度的方向是该点所在位置切线方向,线速度表示的是物体运动的快慢。
匀速圆周运动
如果物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
匀速圆周运动的线速度方向是时刻变化的,所以此处的匀速指的是速度大小不变,其方向时刻发生变化。
角速度
做圆周运动的物体,单位时间内,物体与圆心的连线转过的角度。ω=Δθ/Δt,单位rad/s,
角速度是矢量,但是不要求掌握其方向。角速度表示的是物体转动的快慢。
匀速圆周运动的角速度的大小和方向都不变。
周期
圆周运动中,质点转过一周所用的时间,表示为T,单位s。
频率
圆周运动中,质点每秒转过的圈数,表示为f,单位Hz(s-1).
周期和频率的关系, f=1/T。
转速
单位时间内转过的圈数,转速n的单位是r/s(转每秒)或r/min(转每分),注意同角速度区别。
线速度与角速度的关系
因为时间Δt内,质点运动的弧长Δs=Δθ*r,r是质点做圆周运动的半径。所以
v=Δs/Δt=Δθ*r /Δt=ω*r,即v=ω*r。
变速圆周运动
竖直平面内绳或杆转动小球、竖直平面内的圆锥摆运动等,对于非匀速的圆周运动,一般采取,分析瞬时时刻时,使用匀速圆周运动的规律,分析过程时,使用功能关系。

向心力和向心加速度
从运动性质上来说,匀速圆周运动是变速运动(v方向时刻在变),而且是变加速运动(a方向时刻在变)。物体做匀速圆周运动,那么必然受力不平衡,必须有外力提供向心力,向心力的大小为F=mv2/r;
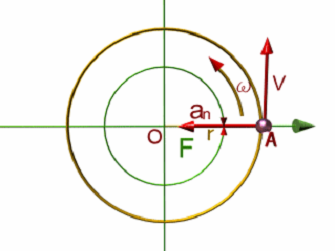
圆周运动向心力和向心加速度
向心加速度的定义a = v2/r;
同时也可证明a =(2π) 2r/T2;
向心力的定义F = mv2/r;
也可表示为F=mω2r(v是线速度,ω是角速度)
向心力的提供者
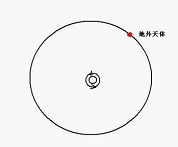
重力或者万有引力提供向心力,比如地球的卫星。
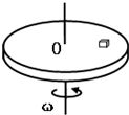
静摩擦力提供向心力,比如木块在圆盘上随圆盘一起转动。
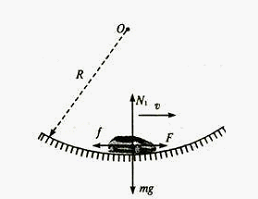
合力提供向心力,比如拱形桥上的车,或者连接凹形坑。
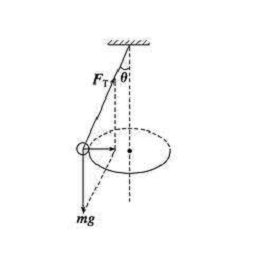
某一个力的分力提供向心力,比如圆锥摆,向心力是由绳的水平分力提供。
向心力由弹力提供,比如水平面上用绳拴着的小球做圆周运动。

牛顿第二定律在圆周运动中的应用
做圆周运动物体所受的向心力和向心加速度的关系同样遵从牛顿第二定律:Fn=ma在列方程时,根据物体的受力分析,在方程左边写出外界给物体提供的合外力,右边写出物体需要的向心力(可选用
等各种形式)。
(1)做匀速圆周运动物体所受的合力为向心力。”向心力”是一种效果力。可以是一个力,也可以是几个力的合力,只要其最终效果是使物体做匀速圆周运动的,都可以作为向心力。
(2)一般地说,当做非匀速圆周运动物体所受的合力不指向圆心时,可以将它沿半径方向和切线方向正交分解,其沿半径方向的分力为向心力,只改变速度的方向,不改变速度的大小;其沿切线方向的分力为切向力,只改变速度的大小,不改变速度的方向。
如果沿半径方向的合外力大于做圆周运动所需的向心力,物体将做向心运动,半径将减小;如果沿半径方向的合外力小于做圆周运动所需的向心力,物体将做离心运动,半径将增大。
(3)圆锥摆是运动轨迹在水平面内的一种典型的匀速圆周运动。其特点是由物体所受的重力与弹力的合力充当向心力,向心力的方向水平。也可以说是其中弹力的水平分力提供向心力(弹力的竖直分力和重力互为平衡力)。
(4)竖直面内圆周运动最高点处的受力。过程分析使用机械能守恒,物体做圆周运动的速率时刻在改变,物体在最高点处的速率最小,在最低点处的速率最大,在某一点分析使用圆周运动的公式。
(5)汽车在水平面内转弯、物体随转盘做匀速圆周运动等,这两种情况下,都是静摩擦力充当向心力。
