平抛运动的概念

    物体以一定的初速度沿水平方向抛出，如果物体运动中仅受重力作用，这样的运动叫做平抛运动。平抛运动是匀变速曲线运动。

    

 

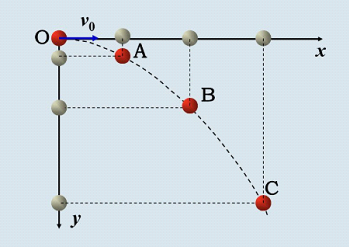
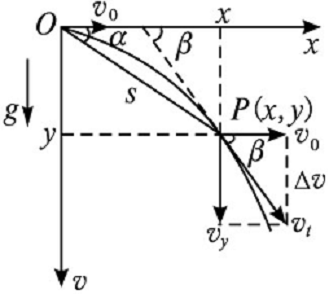
    以抛出点为坐标原点O，以初速度v₀方向为x轴正方向，竖直向下为y轴正方向，建立直角坐标系如图所示．设平抛后t时刻物体的位置坐标为P(x，y)，速度为v_t，t段时间位移为s.

 

     

平抛运动的速度规律
（2）平抛运动的分速度公式

    

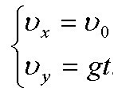
    t时刻的速度大小：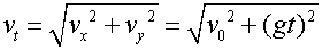
    方向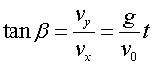： (β为速度与水平方向夹角)
    落地速度只由初速度v₀和运动时间t决定．

一叨诀
    首先要把平抛运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动，然后分别运用两个分运动的规律求分速度、分位移等，再合成得到平抛运动的速度、位移等．

2.平抛运动的位移规律

    平抛运动的位移公式

    
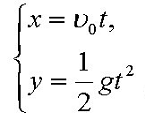
时间 t 内位移的大小：，
    方向： (α为位移与水平方向夹角)．

     注：不能用运动学公式v＝v₀＋gt或v²=v₀²+2gl求解瞬时速度v和位移l，因为平抛运动是曲线运动，而不是匀变速直线运动．

一叨诀
    做平抛运动的物体，速度方向的反向延长线过水平位移x的中点，这个结论在今后的解题中有着重要的应用，应引起足够的重视．

3.平抛运动的时间
    平抛运动的时间由竖直方向上的自由落体运动决定．

    平抛运动在空中的运动时间仅与下落的高度h有关，与初速度v₀无关．

4.平抛运动的轨迹
   做平抛运动的物体，在水平与竖直两个方向上的位移公式如下：

    水平方向x=v₀t；（1）

    竖直方向y=½gt²；（2）

    把(1)中的t=x/v₀带入到(2)中，不难得到这样的结论y=gx²/（2v₀²），

    我们可以将其写成y=kx²的形式；其中k=g/(2v₀²)。

    显然，y与x这两个位移量之间是二次线性关系，且此函数图像过原点。这个二次函数（y=ax²+bx+c）的特点是b和c均为零。

    因此可以看出平抛运动的轨迹是一条顶点在原点，开口向下的抛物线（向下是因为y取向下为正方向）．

    其轨迹方程为：.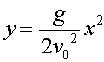

    

 

5.平抛运动的三种典型轨迹分析

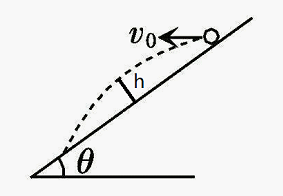
    （1）落到斜面上

    物体从斜面上平抛出后又落到斜面上，如下图所示

    需写出唯一方程，这种情况下在落点满足y和x的比例，等于斜面倾角θ的正切值。

    

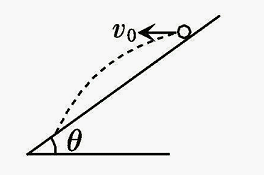
    （2）垂直打到斜面上

    示意图如图所示，这种情况下要从速度方程入手。题中的垂直落到，指的是速度的问题，速度的方向与斜面所在直线垂直。因此，满足的是在落点，物体的合速度方向与水平速度方向的夹角与斜面夹角互余。

    

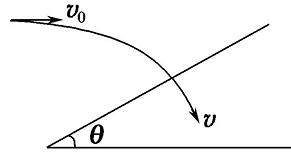
    （3）距离斜面最远

    示意图如下图所示，这种情况下，满足的是B点合速度的方向与斜面方向平行。

    从A点到B点，物体的始终在偏离斜面，而从B点到C点物体始终在接近斜面。因此，在B点时，物体距离斜面最远。此时合速度与水平方向的夹角等于斜面的夹角。