一、简谐运动的描述
(1)描述简谐运动的物理量
①位移x:由平衡位置指向质点所在位置的有向线段,是矢量.
②振幅A:振动物体离开平衡位置的最大距离,是标量,表示振动的强弱.
③周期T和频率f:物体完成一次全振动所需的时间叫周期,而频率则等于单位时间内完成全振动的次数,它们是表示震动快慢的物理量.二者互为倒数关系.
(2)简谐运动的表达式:
x=Asin(ωt+φ)=Asin(2π/T·t+φ)=Asin(2πf·t+φ).
含义:
①x为振动质点相对平衡位置的位移,t表示振动时间。
②A为振动物体离开平衡位置的最大距离,即振幅。
③ω叫简谐运动的圆频率,它也可以表示振动的快慢,圆频率与周期T和频率f的关系为ω=2π/T=2πf
④φ表示t=0时,简谐运动质点所处的状态,称为初相位或者初项。
⑤ωt+φ表示做简谐运动的物体在t时刻处于一个运动周期中的哪个状态,代表简谐运动的相位。
⑥相位差:两个相位之间的差,经常用到两个具有相同频率的简谐运动的相位差,反映的是两个简谐运动的步调差异,如果两个相同圆频率ω的简谐运动1和2的初相位φ1和φ2,则其相位差为△φ=φ1–φ2,相同频率的两个简谐运动有确定的相位差,频率不同的两个简谐运动不具有确定的相位差。
(3)简谐运动的图象
①物理意义:表示振子的位移随时间变化的规律,为正弦(或余弦)曲线.
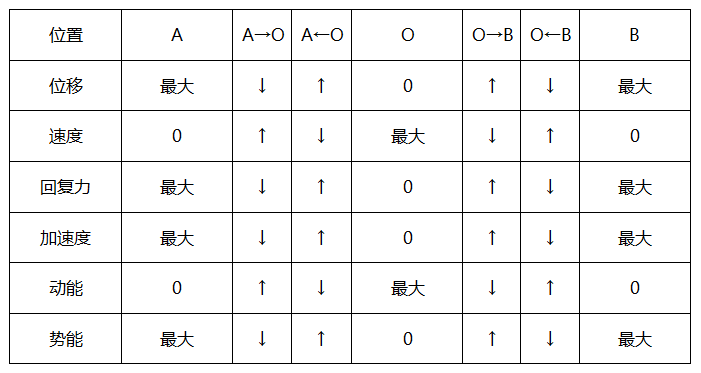
②从平衡位置开始计时,函数表达式为x=Asinωt,图象如图1所示.
从最大位移处开始计时,函数表达式为x=Acosωt,图象如图2所示.
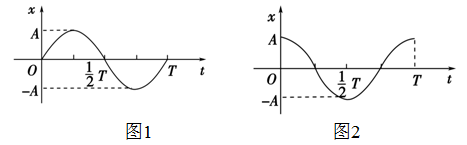
二、回复力
(1)回复力:振动的物体偏离平衡位置后,所受到指向平衡位置的力,叫做回复力。
回复力是根据作用效果命名的,可以是弹力,也可以是其他力(包括摩擦力),可以是几个力的合力(竖直弹簧振子),也可以是几个力的分力(单摆的回复力),回复力为0的位置时平衡位置,但是合外力在平衡位置不一定为0,比如单摆。
(2)回复力的大小:F=-kx,其中F是回复力的大小,k是劲度系数,x是偏离平衡位置的位移,负号表示回复力总是和位移的方向相反。
(3)简谐运动的动力学特征,加速度a=-kx/m,简谐运动是一种变加速的往复运动。
三、简谐运动的能量
(1)定义:做简谐运动的物体在振动中经过某一个位置时所具有的势能和动能的和,称为简谐运动的能量。
(2)变化规律:只有动能和势能的相互转化,对于弹簧振子而言,机械能守恒。
(3)简谐运动的能量与振幅有关,对同一个振动系统而言,振幅越大,能量越大。
(4)振动过程中能量保持不变,没有能量损耗,振动将永不停息的进行下去。
(5)一个振动周期内,动能和势能完成两次周期性变化,经过平衡位置时的动能最大,势能最小,经过最大位移是,势能最大,动能最小。
(6)一个振动周期内,如图所示的振动系统各个物理量的变化如下:

水平的弹簧振子,O为平衡位置,最大位移点是A和B。