一、带电粒子在匀强磁场中的运动

1．若v∥B，带电粒子不受洛伦兹力，在匀强磁场中做匀速直线运动．

2．若v⊥B，带电粒子仅受洛伦兹力作用，在垂直于磁感线的平面内以入射速度v做匀速圆周运动．

3．带电粒子在磁场中初速度v（v⊥B），磁感应强度为B，电荷量为q，粒子质量为，运动公式：

（1）轨道半径：由洛伦兹力提供向心力，有，得到轨道半径。

（2）周期：由轨道半径 与周期之间的关系，得。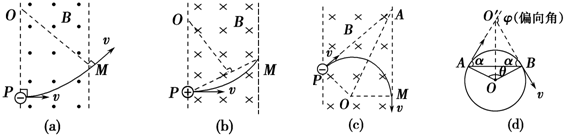

（3）由上公式可知，轨道半径r与速度v成正比，周期T与初速度v无关，只与比荷q/m有关，比荷即电荷q与质量m之比。

 

二、粒子做圆周运动

1、确定圆心：

（1）如图（a）所示，由两点和两线确定圆心，画出带电粒子在匀强磁场中的运动轨迹．确定带电粒子运动轨迹上的两个特殊点（一般是射入和射出磁场时的两点），过这两点作带电粒子运动方向的垂线（这两垂线即为粒子在这两点所受洛伦兹力的方向），则两垂线的交点就是圆心．

（2）如图（b）所示，若只已知过其中一个点的粒子运动方向，则除过已知运动方向的该点作垂线外，还要将这两点相连作弦，再作弦的中垂线，两垂线交点就是圆心．

（3）如图（c）所示，若只已知一个点及运动方向，也知另外某时刻的速度方向，但不确定该速度方向所在的点，此时要将其中一速度的延长线与另一速度的反向延长线相交成一角（∠PAM），画出该角的角平分线，它与已知点的速度的垂线交于一点O，该点就是圆心．

2、确定半径

方法一：由物理方程求：半径。

方法二：由几何方程求：一般由数学知识（勾股定理、三角函数等）计算来确定．带电粒子在有界磁场中的常用几何关系

（1）四个点：分别是入射点、出射点、轨迹圆心和入射速度直线与出射速度直线的交点．

（2）三个角：速度偏转角、圆心角、弦切角，其中偏转角等于圆心角，也等于弦切角的2倍．

 

3、确定圆心角与时间

（1）速度的偏向角φ=圆弧所对应的圆心角（回旋角）θ=2倍的弦切角α，如图（d）所示．

（2）时间的计算方法．

方法一：由圆心角求，t=Tθ/2π；

方法二：由弧长求，t=s/v．

 

4、解题思路分析

（1）画轨迹：即确定圆心，利用几何方法画出半径及运动轨迹。

（2）找联系：半径与磁感应强度、运动速度相联系；偏转角与圆心角、运动时间相联系；在磁场中运动的时间与周期相联系。

（3）用规律：即牛顿第二定律和圆周运动的规律，特别是周期半径的表达式。

 

三、常见情形

1、直线边界（粒子进出磁场具有对称性）

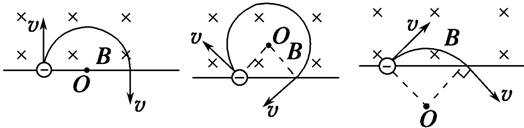
2、平行边界（粒子运动存在临界条件）

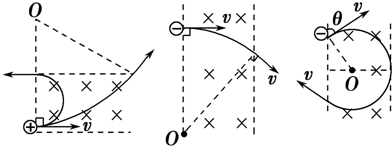
3、圆形边界（粒子沿径向射入，再沿径向射出）