弹簧振子

一、振动

1、定义：物体（或物体的某一部分）在某一位置两侧所做的往复运动，叫做机械振动，通常简称为振动。

 

2、振动的说明

（1）振动的轨迹：振动物体可能做直线运动，也可能做曲线运动。其轨迹可能是直线，也可能是曲线。

（2）振动的特征：往复性。振动具有往复性，周期性重复的运动。

（3）平衡位置：振动的物体能够静止的位置，在该位置物体在振动方向上的合外力为0。

（4）振动的条件：每当物体离开平衡位置后，他就受到一个指向平衡位置的力，该力使物体产生回到平衡位置的效果，受到的阻力足够小。

 

二、弹簧振子

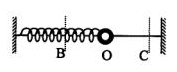
1、定义：如图所示，如果杆上套着一个球，球杆之间摩擦力可以忽略，且弹簧的质量相对于小球也可以忽略，则小球与弹簧组成的系统称为弹簧振子。

2、形式：其他的弹簧振子，比如，竖直方向的弹簧振子。

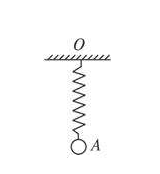
3、弹簧振子是理想化的模型，是由一个没有质量的弹簧一段固定，另一端连接一个质点，振动过程沿着弹簧方向，且过程中没有其他任何摩擦力和阻力。

4、弹簧振子的位移时间图像

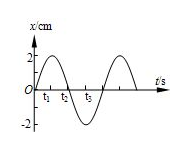
（1）图像横轴表示弹簧振子振动的时间，纵轴表示振子相对于平衡位置的位移。

（2）物理意义：振动图像表示物体相对平衡位置的位移随振动时间的变化规律。

 

简谐运动

1．定义：如果质点的位移与时间的关系遵从正弦函数的规律，即它的振动图象是一条正弦曲线，这样的振动叫简谐运动。

2．简谐运动的描述 
（1）描述简谐运动的物理量 
①位移x：由平衡位置指向质点所在位置的有向线段，是矢量。 
②振幅A：振动物体离开平衡位置的最大距离，是标量，表示振动的强弱。 
③周期T和频率f：物体完成一次全振动所需的时间叫周期，而频率则等于单位时间内完成全振动的次数，它们是表示振动快慢的物理量。二者互为倒数关系。 
（2）简谐运动的表达式x=Asin（ωt+φ）。
（3）简谐运动的图象 
①物理意义：表示振子的位移随时间变化的规律，为正弦（或余弦）曲线。 
②从平衡位置开始计时，函数表达式为x=Asinωt，图象如图1所示。 
从最大位移处开始计时，函数表达式为x=Acosωt，图象如图2所示。 

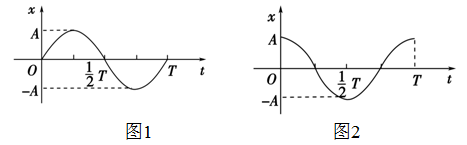
3．简谐运动的回复力 
（1）定义：使物体返回到平衡位置的力。 
（2）方向特点：回复力的大小跟偏离平衡位置的位移大小成正比，回复力的方向总指向平衡位置，即F=-kx。

4．简谐运动的能量 
简谐运动过程中动能和势能相互转化，机械能守恒，振动能量与振幅有关，振幅越大，能量越大。

5．简谐运动的两种基本模型

	弹簧振子（水平）	单摆
模型示意图
条件	忽略弹簧质量、无摩擦等阻力	细线不可伸长、质量忽略、无空气等阻力、摆角很小
平衡位置	弹簧处于原长处	最低点
回复力	弹簧的弹力提供	摆球重力沿与摆线垂直（即切向）方向的分力
周期公式	（不作要求）
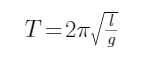能量转化	弹性势能与动能的相互转化，机械能守恒	重力势能与动能的相互转化，机械能守恒