运动的合成和分解

1．分运动和合运动

一个物体同时参与几个运动，参与的这几个运动即分运动，物体的实际运动即合运动． 

2．运动的合成与分解 
已知分运动求合运动称为运动的合成；已知合运动求分运动称为运动的分解．两者互为逆运算．在对物体的实际运动进行分解时，要根据实际效果分解．

 
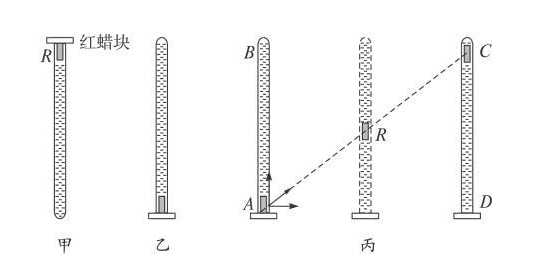
3．遵循的规律 
位移、速度、加速度都是矢量，故它们的合成与分解都遵循平行四边形定则．
（1）如果各分运动在同一直线上，需选取正方向，与正方向同向的量取“+”号，与正方向反向的量取“-”号，从而将矢量运算简化为代数运算．
（2）两分运动不在同一直线上时，按照平行四边形定则进行合成，如图所示．

4．运动分解的步骤：

分解的原则：按照运动的实际效果分解．

（1）确定合运动的方向（实际运动方向）．

（2）分析合运动的运动效果．

（3）依据合运动的效果确定分运动的方向．

（4）利用平行四边形定则、三角形定则或者正交分解法作图，将合运动的速度、位移、加速度分别分解到分运动的方向上．

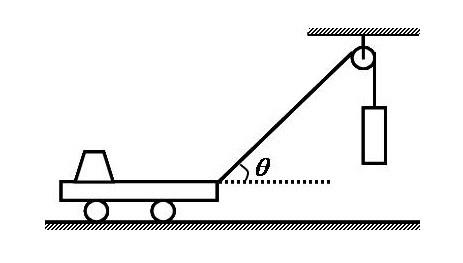
5．合运动和分运动的关系 
（1）等时性：合运动与分运动经历的时间相等．
（2）独立性：一个物体同时参与几个分运动时，各分运动独立进行，不同方向上的分运动互不干扰．
（3）等效性：各分运动叠加起来与合运动有完全相同的效果． 
（4）同体性：合运动与分运动是对同一个物体而言的．

 

6．合运动的性质与轨迹
 合运动的性质和轨迹，由两个分运动的性质及合初速度与合加速度的方向关系决定． 
（1）根据加速度判定合运动的性质：若合加速度不变，则为匀变速运动；若合加速度（大小或方向）变化，则为非匀变速运动．
（2）根据合加速度的方向与合初速度的方向判定合运动的轨迹：若合加速度的方向与合初速度的方向在同一直线上则为直线运动，否则为曲线运动．
（3）合力（或合加速度）方向与轨迹的关系

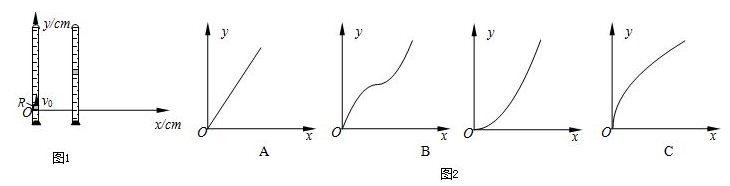
物体做曲线运动的轨迹一定夹在合力（或合加速度）方向和速度方向之间，速度方向与轨迹相切，合力（或合加速度）方向指向曲线的凹侧．